Un peu de géométrie – partie 1

En pavage de plan on utilise des formes colorées en les agençant de telle façon que ces formes tapissent le plan sans espace mais aussi sans superposition de celles-ci.

C’est une redite de l’article précédent dans lequel j’en parlais déjà.

Mais qu’est-ce qu’une forme ?

En mathématique on peut considérer une forme comme une figure combinée par un nombre fini de points et de segments et/ou des courbes les reliant; on peut ajouter : délimitant des surfaces et permettant des comparaisons de longueurs et d’angles et si besoin de courbures. On peut considérer une forme à partir de 2 points puisqu’on peut à partir de ces deux points tracer un segment de droite entre ceux-ci.

Une forme peut aussi être défini par le rapport entre deux motifs. En exemple, si un triangle a les mêmes angles qu’un autre triangle on peut dire qu’il est de même forme que cet autre triangle; par contre, cette condition n’est pas suffisante pour un rectangle dont il faut aussi calculer les rapports des segments pour vérifier qu’ils sont identiques.

Un peu de géométrie - partie 1-1

On parle généralement d’une forme à partir d’une représentation d’un objet ayant trois points et là on aborde la notion de surface. puisqu’en-dessous de trois point on n’a qu’une longueur pour le segment de droite et pour un point on a… un simple point.

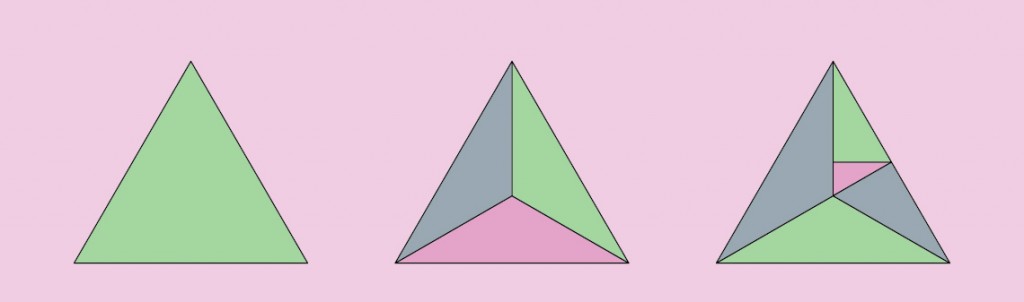
Tous les objets ayant trois points et plus sont divisibles en formes de trois points. Cette division n’est pas forcément unique et peu continuer à l’infini car chaque triangle est lui-même divisible en deux parties ou plus, qui eux-même sont divisibles, etc.  Tout triangle peut par cette division donner naissance à 2 triangles rectangles.

On peut à partir de ce qui est dit précédemment diviser tout objet topologique en triangles définis (positions des points longueurs des segments et valeurs des angles de ces triangles). On utilise ces particularités pour définir la surface d’un objet quelconque. La topologie est la branche des mathématiques qui étudie les relations de position dans l’espace et aide à définir les propriétés des objets étudiés.

Plus précisément, c’est une partie de la géométrie. Les topologues sont les mathématiciens s’occupant de cette branche des mathématiques. L’usage le plus courant de la topologie est le calcul de distances et de surfaces et éventuellement de courbures qui sont réalisés par les géomètres topographes pour le domaine foncier (calcul de surfaces d’une propriété, division parcellaire de celle-ci, bornage d’un terrain pour y construire ou le clôturer, respects des lois dans le domaine de la propriété) et de génie civil (cartographie, construction d’une route ou d’une ligne de chemin de fer, création d’un ouvrage — pont, tunnel, station de métro —, passage de conduites techniques en milieu urbain ou en campagne, etc.). Mais aussi le calcul des dénivelés.

Comme je disais dans l’article précédent la division du plan en parcelles existe certainement depuis la sédentarisation des hominidés et le besoin de contrôler et de régir les sociétés. Les moyens au départ intuitifs de calculs ont donné naissance je suppose à des techniques et des outils qui eux-même peu à peu ont donné naissance à la géométrie; cela se complexifiant à chaque nouveau besoin de l’homme. Je lisais dernièrement que le théorème de Pythagore était certainement beaucoup plus ancien qu’on ne le pensait jusqu’à maintenant après avoir trouvé une tablette babylonienne (réf. IM67118) datant de 1 700 av. J.-C. sur un site de fouille en Irak en 1962 et qui citerait les mêmes éléments de preuves et de définition que ceux de Pythagore. Je reste prudent malgré tout mais je ne doute pas de cette possibilité au regard d’autres tablettes (YBC 7289, YBC 7243) traitant du même sujet et de façon nettement plus complexe que la simple relation de la diagonale du carré à ses cotés. liens ci-dessous.

YBC-7289-REV YBC-7289-OBV

figure : tablette babylonienne YBC 7289

Presque deux millénaires plus tard, les romains ont créés des ouvrages importants sur ces principes géométriques qui sont parvenus jusqu’à nous et nous donne des leçons en matière d’écologie et de productivité. Les sites du pont du Gard mais surtout de son canal de 50 km qui amenait l’eau potable à Nîmes d’une source de montagne avec un dénivelé moyen de 25 cm par kilomètre soit uniquement 12,60 m sur l’ensemble du parcours, l’aqueduc de Montjeu, beaucoup plus court mais qui permettait aussi par des astuces incroyables d’amener l’eau potable à Autun, une autre grande ville romaine qui n’a malheureusement pas gardé ses monuments. Un autre site intéressant est le site de l’aqueduc et des moulins de Barbegal, proche d’Arles et de Fontvieille. Malheureusement il ne reste là encore plus grand chose à voir des moulins; restent des parties de l’aqueduc et une vue sur la vallée qui laissent imaginer la majesté de ce site en son temps.

Ces sites sont des exemples parmi d’autres de réalisations ayant demandé de fortes connaissances en géométrie et au même titre que le travail du géomètre actuel les relevés topographiques pour la réalisation de ces ouvrages et de tant d’autres (dont les milliers de voies romaines au travers de l’Europe et de tous les pays méditerranéens montre qu’une connaissance approfondie des principes de géométrie et de topologie étaient déjà fortement ancrés dans les usages dès cette époque.

Je passe mais le monde romain est certainement la civilisation qui a le plus utilisé la géométrie dans ses ouvrages. L’ensemble de ce qui nous reste à voir et à comprendre autour de la Méditerranée est suffisamment conséquent et pour certains bâtiments, cela nous donne encore des leçons de leur génie deux mille ans après.

J’en reviens à nos surfaces. En France la modification des systèmes d’impositions au XVIIème siècle et la nécessité de connaitre pour cela les terres possédées par chacun sous Louis XIV et ensuite les guerres napoléoniennes ont permis par un effort important la réalisation d’un cadastre pour connaitre aussi la superficie totale de la France.

Et maintenant revenons à nos moutons : nos formes. Je disais tout à l’heure que chaque forme pouvait être décomposée en de multiples triangles et la limitation n’est que la taille minimale de chaque triangle que l’on veut créer. Si on fait des gros triangles on aura une grossière approximation de notre forme, ou alors notre forme sera suffisamment simple pour être réduite seulement de cette façon et il n’y a pas besoin de chercher plus loin ou plutôt… plus petit.

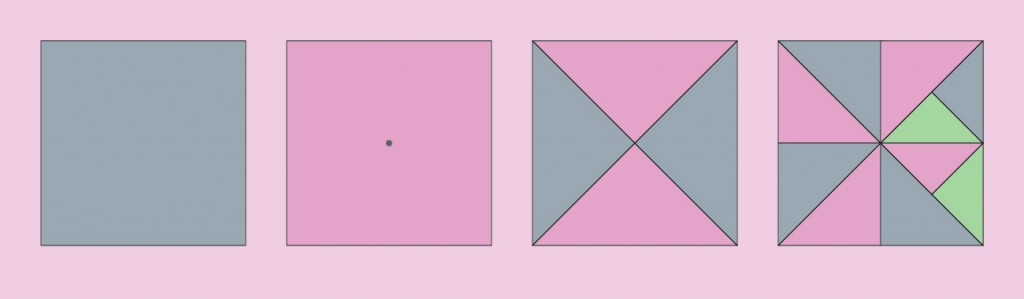
Un peu de géométrie - partie 1-1

Un carré par exemple peut-être réduit en seulement 4 triangles droits identiques en ajoutant un simple point au centre de ce carré. Dans ce cas, chaque triangle étant lui-même un demi-carré de coté égal à la moitié de l’hypoténuse du carré d’origine et son hypoténuse égal au coté de ce même carré. On peut reproduire la division sur ces triangles pour obtenir les mêmes formes réduites et ce à l’infini.

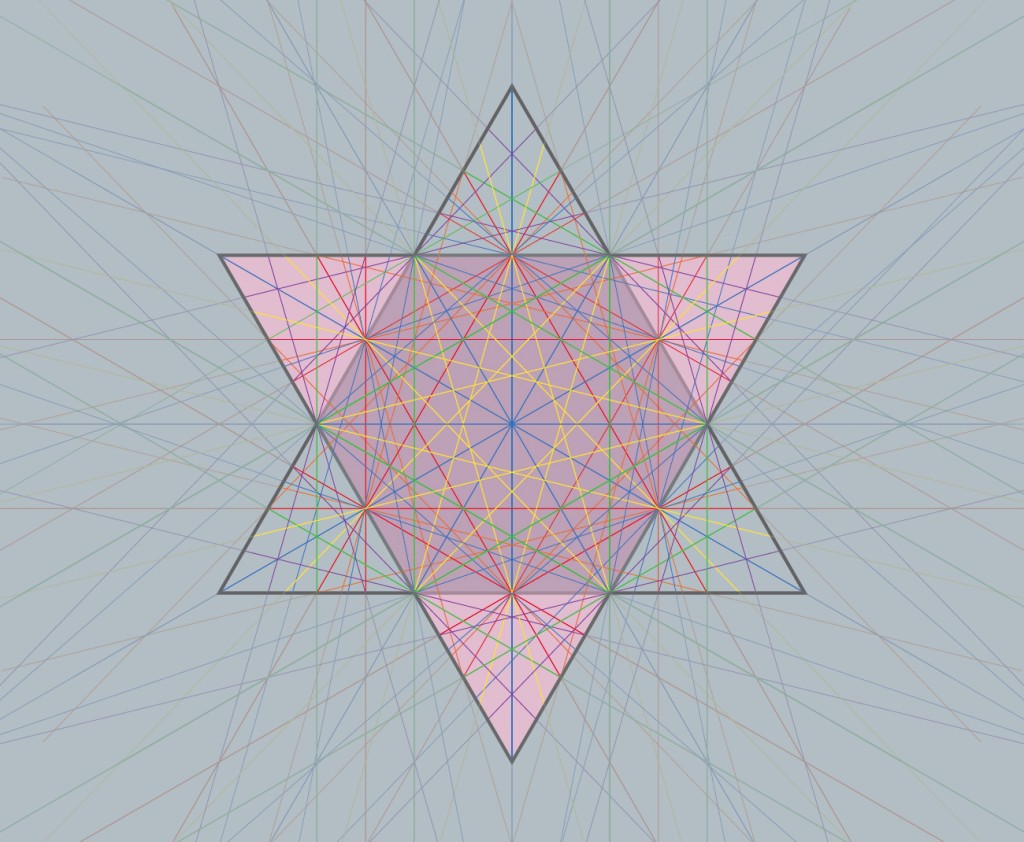
Les artisans et mathématiciens arabes du début du second millénaire ont utilisé la même façon de penser pour créer des centaines de formes que sont les zelliges. Avec deux formes de base, triangle et carré, ils ont réalisés les autres formes en se basant sur les angles, la superposition et l’inclusion ou l’exclusion de ce qui dépasse ou de ce qui est doublé. Il suffit de prendre ces deux formes dans Inkscape, Illustrator ou peut-être même Canva et de s’appliquer à quelques manipulations et quelques applications d’effets pour voir les possibilités de cette technique. On verra par la même occasion, l’apparition d’un nombre de triangles de plus en plus importants au fur et à mesure de ces tripatouillages.

dessin zellige

Cet exemple montre bien la complexité déjà présente lors de la superposition de deux triangles. Le nombre possible de lignes pour relier les points caractéristiques de ceux-ci (angles, points de croisement des segments) est déjà très important et peut engendrer de multiples formes et motifs. Je n’ai fait dans ce dessin que relier chaque point de croisement et chaque point au centre de chaque segment, je n’ai pas utilisé la possibilité d’y ajouter les sommets des triangles ce qui aurait encore complexifié ce dessin.

Je n’ai fait qu’effleurer dans ce premier article le sujet et je n’ai pas encore utilisé une seule valeur d’angle, cela ne devrait pas être le cas dans l’article suivant. En attendant que je l’écrive n’hésitez pas à consultez les quelques liens que j’ai mis ci-dessous.

Suite de l’article ici : Un peu de géométrie – partie 2

quelques références :

sur les babyloniens :

sur les romains :

Autour de Napoléon et du cadastre