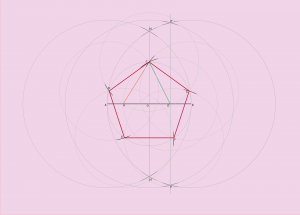
On va réaliser ici une étude relativement complète d’un polygone régulier à 5 cotés ; le pentagone. Si je prends spécifiquement celui-ci plutôt qu’un hexagone ou un octogone c’est parce qu’il est impair, qu’il est complexe à dessiner et que de multiples variantes existent dans sa méthode de construction.

Ceci est la suite de l’article Un peu de géométrie – partie 3

Certaines comme la méthode de Dürer sont des méthodes approximatives permettant un usage rapide dans les arts graphiques par contre comme elles ne sont pas justes, ces dernières ne doivent pas être utilisées en mathématiques, en mécanique ou dans une quelconque science “exacte”.

Comment commencer ?

Certains créent le cercle avant de dessiner le diamètre; de mon coté je pense qu’il faut faire l’inverse pour respecter l’ordre des définitions d’Euclide dans Les Éléments de géométrie.

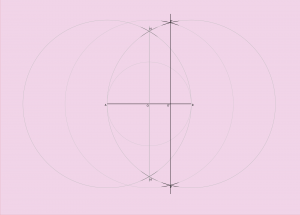
Je dessine donc ma ligne AB d’une dimension au hasard (ou presque) de 350 points de longueur.

Apostilles :

• Pour visualiser correctement les images, penser à cliquer dessus pour les agrandir. La plupart des éléments étant en gris clair et étant relativement fins ne sont pas visibles sur les petites images.
• le cercle C1 n’est pas nommé sur les graphiques mais je pense que vous n’aurez pas de mal à comprendre duquel il s’agit.

 

À partir de cette ligne, je vais dessiner sa perpendiculaire au centre de celle-ci. Je prend donc mon compas que je positionne en début de ligne (point A) et j’écarte celui-ci de la longueur de la ligne (jusqu’au point B). Je vais donc dessiner un cercle de rayon égal à ma longueur de ligne. Une fois cela fait, je fais la même chose en positionnant mon compas en fin de ligne (point B) et je refais un cercle de 350 points de rayon.

 

Mes deux cercles se croisent au-dessus et au dessous de ma ligne AB, je vais me servir de ces deux points pour dessiner ma perpendiculaire.

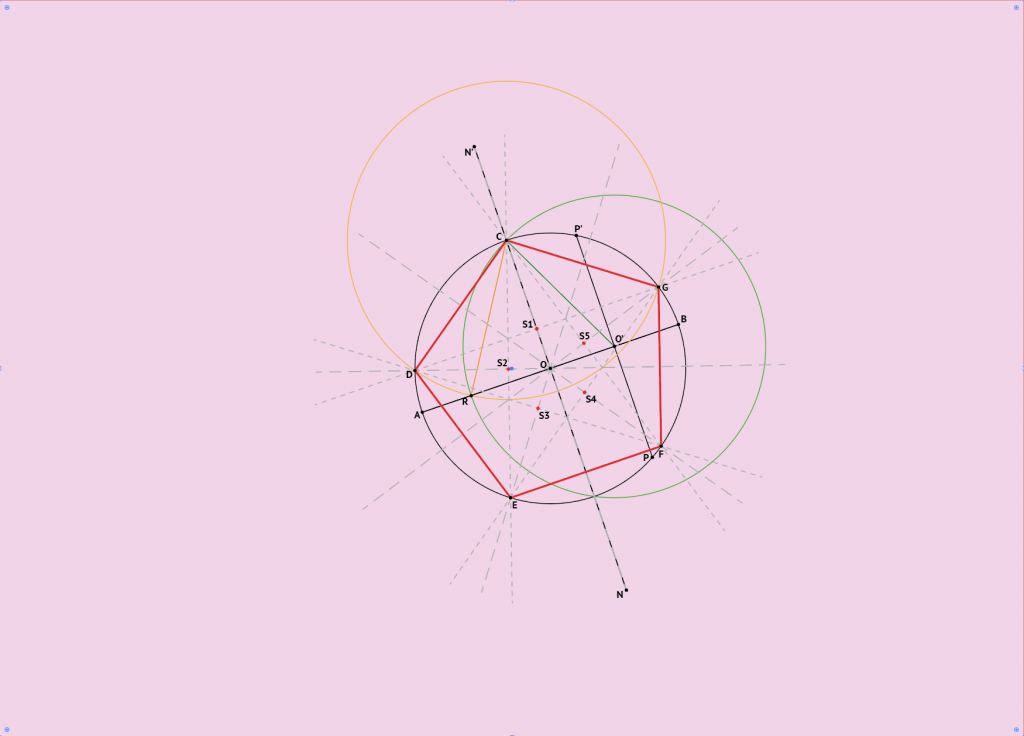
Voilà, c’est fait. J’ai maintenant le milieu de ma ligne de base (point O). Je reprends mon compas et je dessine un cercle C1 de diamètre égal à ma ligne de base. C’est ce cercle qui va supporter mon pentagone.

Arrivé à ce stade, je rentre dans l’inconnu comme vous. Comment dois-je m’y prendre pour avancer dans mon dessin ? Je ne le sais pas. Je vais donc réaliser les différentes étapes et noter toutes les informations qu’on me donne indirectement dans cette méthode et les adapter en conséquence de ma base qui est mon segment de droite de 350 points de longueur.

J’ai donc

• Un segment de droite AB de 350 points de longueur au centre d’un plan de dimensions quelconque (ici 2000 x 2000).
• Le centre de mon plan est au point O en (1000, 1000), ma ligne est donc à 1000 points du haut, 825 points à gauche et va jusqu’à 1175 points à droite.
• J’ai dessiné un cercle de rayon 350 points et dont le centre est le point de début de segment soit en (825, 1000).
• J’ai dessiné un deuxième cercle en (1175, 1000) toujours de 350 points de rayon.
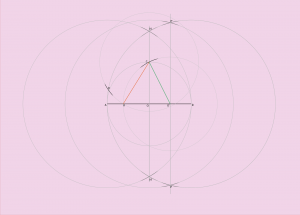
• Cela m’a permis de dessiner un trait perpendiculaire NN’ à mon segment de base et au centre de celui-ci soit en (1000, y), “y” ayant peu d’importance. J’ai donc maintenant correctement visualisé mon point 1000 x 1000.
• Je me sers de ce point pour dessiner un cercle C1 de diamètre égal à mon segment d’origine soit 350.

Je peux maintenant visualiser un autre point utile situé au centre du rayon de mon dernier cercle tracé.

Ici nous pouvons utiliser deux méthodes pour continuer. Soit j’utilise le petit rayon correspondant à un rayon égal à la moitié de mon segment d’origine, soit j’utilise le grand rayon correspondant à mon segment d’origine. J’opte pour cette solution afin d’éviter trop d’encombrement à l’intérieur de ma figure (dans les tableaux de calculs ci-dessous, j’utiliserai le petit rayon).

Ma prochaine étape pour respecter la méthode est de dessiner un point au centre du plus petit rayon. Je dessine donc un grand cercle dont le centre est le centre de mon segment d’origine et du petit cercle. Je réalise donc les même étapes ensuite pour afficher une perpendiculaire à mon segment de base passant par ce point

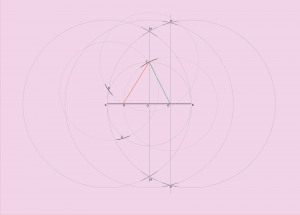
Pour se faire, j’utilise la même méthode que pour visualiser le centre de mon segment en traçant un cercle à la fin de mon rayon car nous avons déjà fait le cercle de début.

  

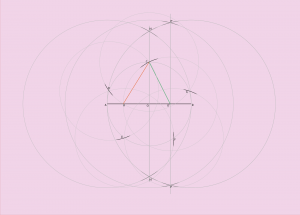
Pour continuer, j’ai maintenant un point sur l’axe PP’ que j’ai appelé O’ et qui va me servir à dessiner un cercle de rayon qui va de ce point O’ au point C qui est un point sur le cercle porteur le cercle porteur du pentagone C1 et aussi sur la médiatrice NN’. Ce point est le premier point de mon pentagone sur le cercle circonscrit C1.

Un fois ce cercle dessiné, je peux maintenant placer le point R qui se trouve au croisement de notre dernier cercle et de la droite AB. J’utilise ce point R pour dessiner un cercle de centre C et de rayon OR. Ce cercle croise le cercle C1 au point D; ce point sera le deuxième point de notre pentagone.

  

On peut en déduire maintenant que CD est la longueur d’un segment de notre pentagone, il suffit maintenant de mettre notre compas en D et de tracer un cercle pour pouvoir placer le point E puis on fait de même en E pour obtenir le point F; Puis en F pour obtenir le point G.

  

Si votre dessin est correct, vous devriez maintenant, par un dernier cercle de centre G, revenir à votre point C.

Lorsque vous dessinez les différents cercles permettant de complémenter les points d’angles de notre pentagone chaque cercle passe deux fois sur le plus petit cercle, le premier point sert à placer le nouveau point mais le deuxième doit-être identique au centre précédent. Donc si cela ne se fait pas correctement, vérifier vos mesures et/ou l’écartement de votre compas.

Pour finir notre figure, il suffit maintenant de tracer les segments, CD, DE, EF, FG et GC et de nettoyer notre figure.

  

Je vous ai fait un tableau ci-dessous avec les mesures utilisées dans mes calculs. les valeurs de N, N’, P, P’ n’ont aucune importance, je les ai calculées mais les valeurs de P et P’ sont différentes de celles du point représenté sur le dessin. Les valeurs dans le tableau sont les valeurs des points de croisement d’un cercle de rayon OB et de centre B avec le cercle C1 de même rayon OB et de centre O dessiné auparavant. vous pouvez voir malgré tout les points de croisement du cercle C1 avec ce nouveau cercle dans la droite perpendiculaire dessinée PP’ aux croisements avec C1.

	position
	position donnée			position calculée
point	x	y		x	y
A	825	1000
B	1175	1000
N				1 000	1 303,1089
N’				1 000	696,8911
O	1000	1000		1 000	1 000
P				1 087,50	1 151,5544
P’				1 087,50	848,4456
O’				1 087,50	1 000
C	1000	825		1 000	825,00
R	x	1000		891,8441	1 000
S1				1 000	945,9220
D	x2	y2		833,5651	945,9220
S2				948,5688	983,2890
E	x3	y3		897,1376	1 141,5780
S3				968,2138	1 043,7500
F	x4	y4		1 102,8624	1 141,5780
S4				1 031,7862	1 043,7500
G	x5	y5		1 166,4349	945,9220
S5				1 051,4312	983,2890
vérification de C				1000	825

Les valeurs x, x2, y2, x3, y3, x4, y4, x5, y5 sont à calculer en utilisant le théorème de Pythagore, bien sûr en trouvant d’abord les valeurs des rayons O’C et CR.

	longueur
segment	longueur donnée	formule		longueur calculée
AB				350
AO ou OB		la moitié de AB		175
OO’ ou O’B		la moitié de OB		87,5
OC ou r1		la moitié de AB		175
O’C		hypoténuse du triangle OCO’		195,655948031232
OR		position de O’ moins longueur de O’C		108,155948031232
CR ou r2		hypoténuse du triangle OCR		205,724838302366
d		distance entre les centres O et C		175
a		décalage en x du centre		120,922025984384
b		décalage en y du centre		54,0779740156158
h		longueur du segment passant par Sn et perpendiculaire à OSn		166,434890351652
CD		identique à CR		205,724838302366
DE		identique à CR		205,724838302366
EF		identique à CR		205,724838302366
FG		identique à CR		205,724838302366
GC		identique à CR		205,724838302366

Je vous laisse calculer cela en vous donnant ci-dessous 3 références intéressantes ci-dessous pour y arriver.

Ces tableaux sont intéressants car toutes les formules de calculs sont présentes. Il ne me suffirait maintenant que de changer quelques valeurs — mon point de départ A et ma longueur de segment AB (diamètre du cercle porteur du pentagone C1) — pour obtenir quasiment instantanément l’ensemble des autres valeurs et de pouvoir reporter cela pour un usage quelconque. Je pourrai aussi définir les positions exactes de A et B pour un calcul automatique du segment AB et l’orientation de mon pentagone sera en fonction de ces nouveaux paramètres. La figure ci-dessous est un exemple de cela. Il ne me reste plus qu’à faire un algorithme en javascript par exemple avec une sortie canvas ou SVG pour dessiner automatiquement tout pentagone dont on me donnerait les coordonnées du diamètre du centre et de l’angle ou de la position exacte des points A et B.

Sur ordinateur il est relativement plus simple de dessiner un pentagone. comme on a 5 angles, il suffit de diviser 360° par 5; on obtient 72°. On commence par dessiner un premier coté puis on se place au bout de celui-ci on ajoute dans son alignement un deuxième segment de même longueur qu’on va tourner à 72° dans un sens ou dans un autre. 4 répétitions identiques plus tard et on a son pentagone et cela indépendamment de tout calcul, de la longueur de notre segment de base, de la rotation de départ, etc.

L’intérêt de la méthode au compas est de multiplier les croisements entres les différents cercles et segments de droite qu’on dessine et d’apporter une possible évolution à ce travail. Une autre solution est bien sûr de tirer toutes les lignes partant de chaque angle et de chaque centre comme je l’ai montré dans les parties précédentes.

L’usage de ces méthodes pour trouver une suite possible au motif est importante. Elle peut permettre aussi d’assembler deux motifs ou plus en trouvant une bordure possible entre les motifs.

Ici les angles caractéristiques sont 18°, 36°, 72°, et les angles supérieurs par ajout de 18° chaque fois.

Voilà, je vais arrêter ici cet article mais si vous avez compris la méthode vous pouvez continuer avec des polygones ayant un nombre de cotés et d’angles plus important. Certaines étoiles au centre des motifs ont quelquefois plus de 100 angles et cotés, Cela pour donner les rosaces les plus splendides et variées possibles. Il est à noter que pour certaines des chiffres impairs et premiers tel que 117 ont certainement été un vrai casse tête aux artisans d’Al-Andalus pour la taille des pièces et ne serait-ce que pour le dessin d’étude préalable à cela. Mais comme on dit à cœur vaillant rien d’impossible.

Et voici le grand final de cette série : Création d’un heptagone régulier circonscrit à un cercle

références

Pentagone régulier avec GeoGebra sur le site de Patrice Debart : http://www.debart.fr/geogebra/pentagone_geogebra.html

Comment calculer les points d’intersection de deux cercles ? : https://lucidar.me/fr/mathematics/how-to-calculate-the-intersection-points-of-two-circles

Polygones Pentagones par Gerard Villemin : http://villemin.gerard.free.fr/GeomLAV/Polygone/Pentagon.htm