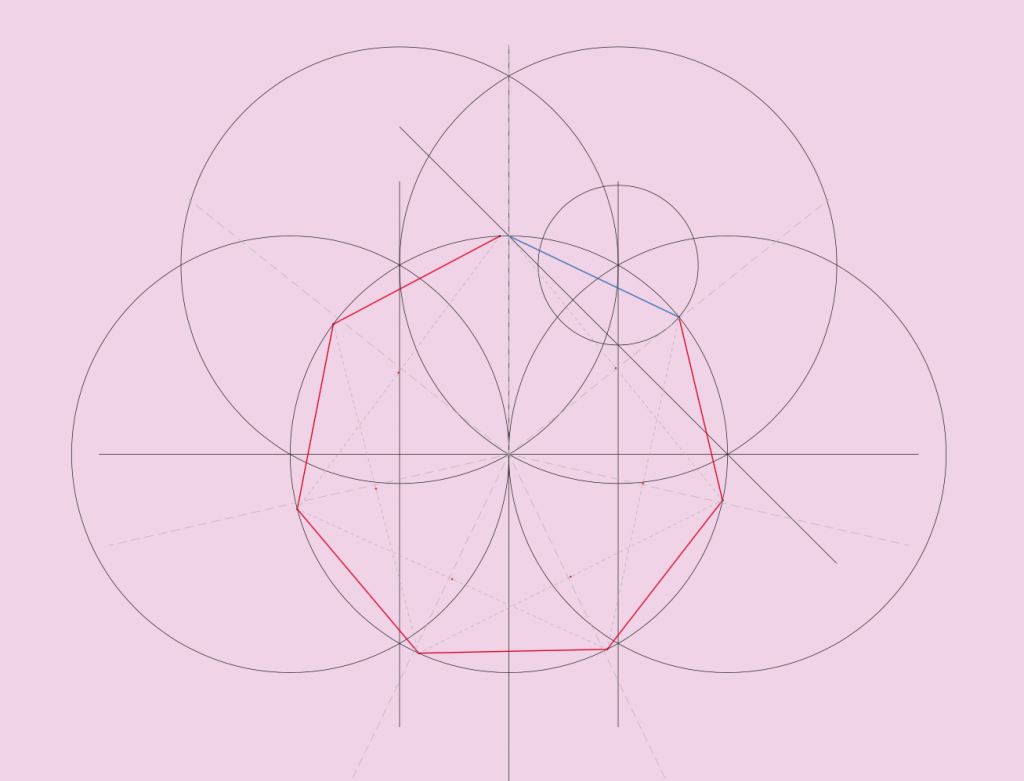
Il est difficile de dessiner un heptagone régulier. J’ai dû m’y reprendre en trois fois et la littérature sur le sujet est moins dense que sur le pentagone et encore moins que pour l’hexagone et l’octogone réguliers.

Ceci est la suite de l’article Un peu de géométrie – partie 4

La première méthode n’était qu’une méthode approximative et avec mes choix de ne presque pas utiliser la trigonométrie et les valeurs d’angle, je ne me suis rendu compte de mon erreur qu’une fois arrivé à la fin du dessin. Vous pouvez voir le décalage important qui fait que même pour une simple représentation l’erreur est trop significative pour un usage graphique.

J’ai donc repris une autre méthode encore plus foireuse mais… ouf ! je m’en suis rendu compte assez tôt cette fois.

Une troisième méthode m’a donné du fil à retordre mais je l’ai finie, j’ai les formules et je pourrais l’utiliser maintenant sur n’importe quel valeur de coté. Celle-ci est simple et compliquée à la fois : simple car elle ne nécessite que peu d’étapes, et compliquée car elle demande un peu de réflexion. Mais quand n’est-ce pas le cas en mathématique et plus précisément en géométrie ?

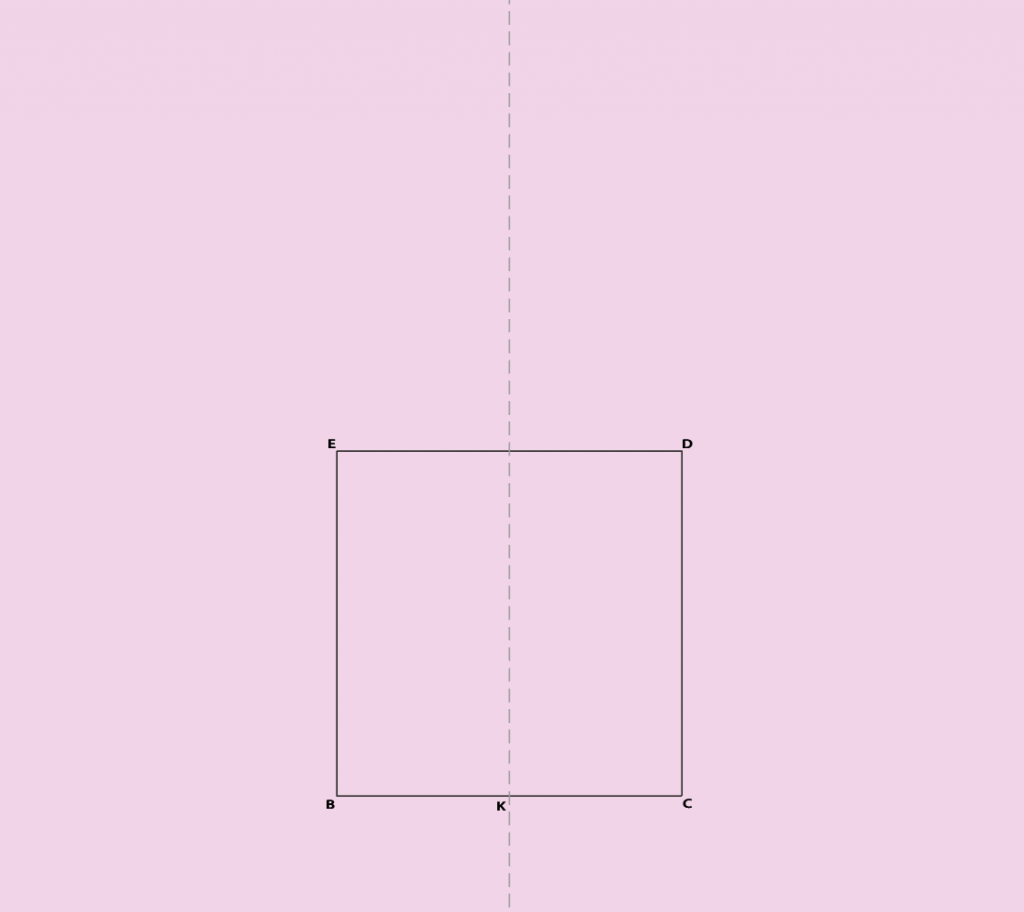
La première étape et la plus importante est de dessiner un triangle isocèle dont la base sera la valeur de nos côtés d’heptagone.

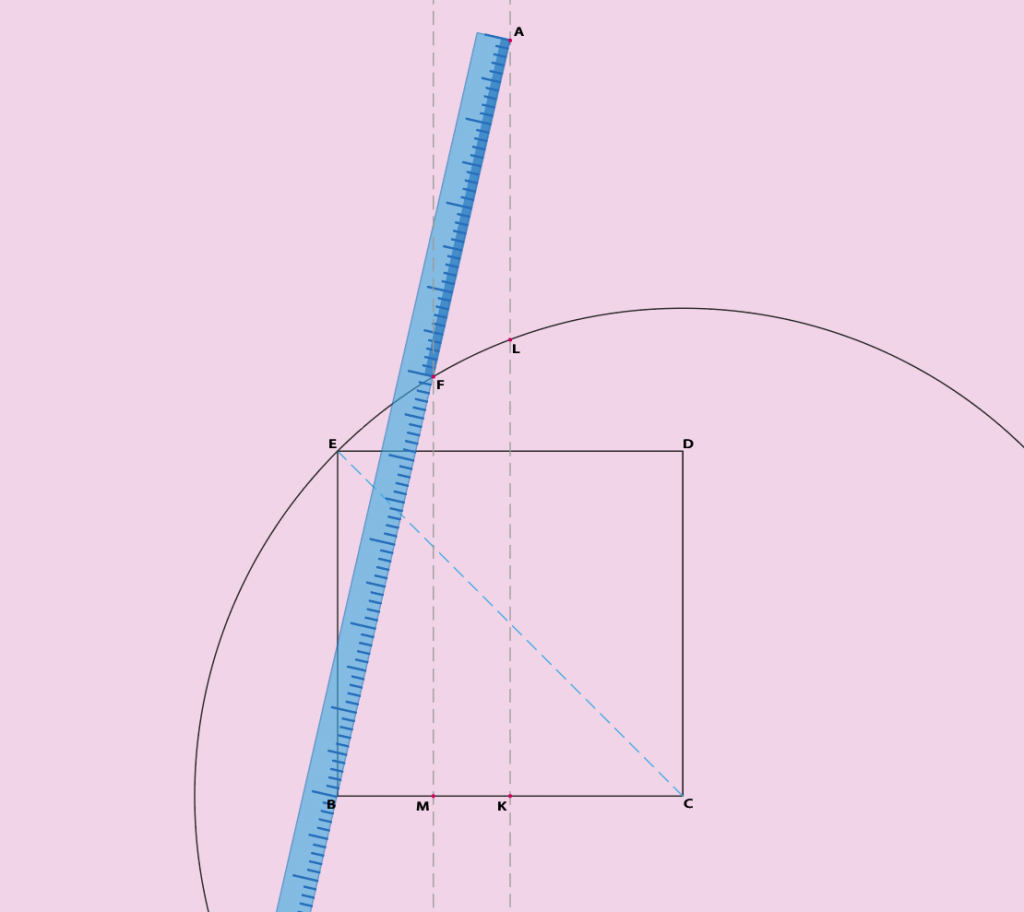
Pour réaliser ce triangle on part d’un simple carré BCDE (pour une construction du carré au compas et à la règle voir l’article Un peu de géométrie – partie 2). Avec BC notre base, le premier des côtés de l’heptagone.

Ensuite on dessine la droite perpendiculaire à BC et passant par son centre K. Je n’explique plus ici comment procéder car je l’ai expliqué plusieurs fois dans l’article en référence ci-dessus. On étend cette ligne au-dessus du carré de façon suffisante pour la suite du dessin.

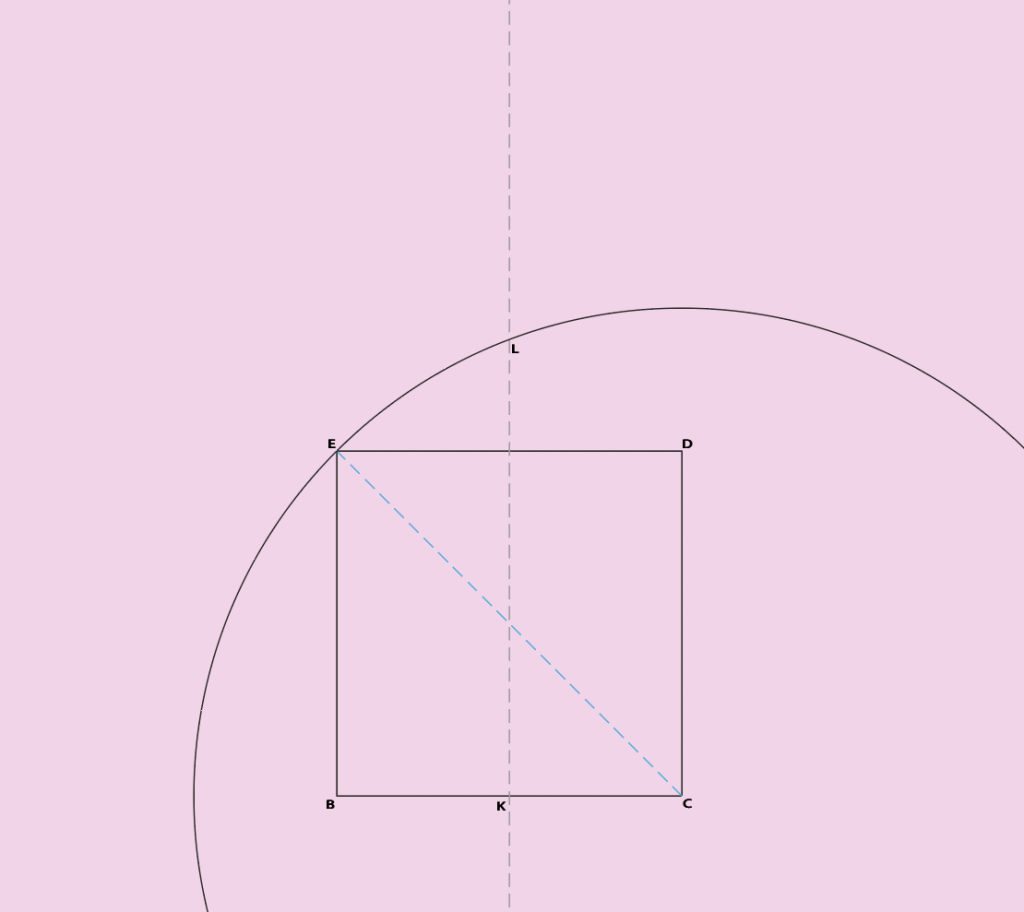
En troisième, on va dessiner un cercle c1 de centre C et dont le rayon est l’hypoténuse de BCE. Ce cercle passera donc par le point E sur le carré, par un point L situé sur la médiatrice de BC. et par un point non encore défini F.

Ce point particulier nous intéresse sur ce cercle. Mais malheureusement on ne peut pas le dessiner au compas car il nécessite de connaître les coordonnées d’un point A sur l’axe KL. Hors ce dernier point ne peut être défini que si on connait la position du point F qui est déjà un point qu’on recherche.

C’est ici l’histoire de la poule et de l’œuf. Et comme dans tout processus d’évolution, c’est le temps et l’expérience qui nous donneront la solution.

Le but de ce point A est qu’avec les points B et C, ils se trouveront tous les trois sur le cercle c2 qui va nous permettre de dessiner notre heptagone. De plus, on a dès à présent le segment de droite BC qui est de fait l’un des côtés de notre heptagone. Tout est déjà en place. Que demander de plus.

On va donc y aller à tâtons en connaissant deux ou trois choses qu’on peut exploiter :

• la distance AF = la distance BC. Pourquoi ? je n’en sais rien, c’est comme cela. En fait si, on sait pourquoi. AF est le rayon du cercle de centre A qui croisera le cercle c2 en deux points, on sait que notre base BC est l’un des cotés de l’heptagone et donc que le point A est sur la médiatrice de BC car le nombre de cotés de l’heptagone est impair et donc qu’à l’opposé de notre coté BC on a un angle et non un autre coté parallèle à BC. Donc si comme dans les autres polygones dont on connait les dimensions et donc le diamètre du cercle circonscrit on pourrait dessiner grâce à un compas notre polygone. Ici ce n’est pas le cas car justement on ne connaît pas ce point A et on ne connaît pas non plus le diamètre du cercle inscrit à ce polygone. On pourrait grâce aux angles obtenir le centre O et le dessiner mais le but est bien de faire le dessin au compas et à la règle sans usage de mesures d’angles.
• A, F et B sont alignés.
• AFC est un triangle dont 1 point est défini (C) de coordonnées (1200, 1200) et 2 longueurs sont définies : AF et CF. AF = BC et CF est égal à l’hypoténuse de EBC (triangle rectangle isocèle).

Comment faire ?

Les anciens avaient la réponse en utilisant la méthode de la construction par neusis.

Qu’est-ce que la construction par neusis ? c’est une méthode qui permet grâce à une règle graduée de trouver deux points et une direction sur un graphe. “Neusis” venant du grec pourrait se traduire par “pencher vers”. Dans notre exemple on va plutôt “redresser vers” mais c’est la même chose.

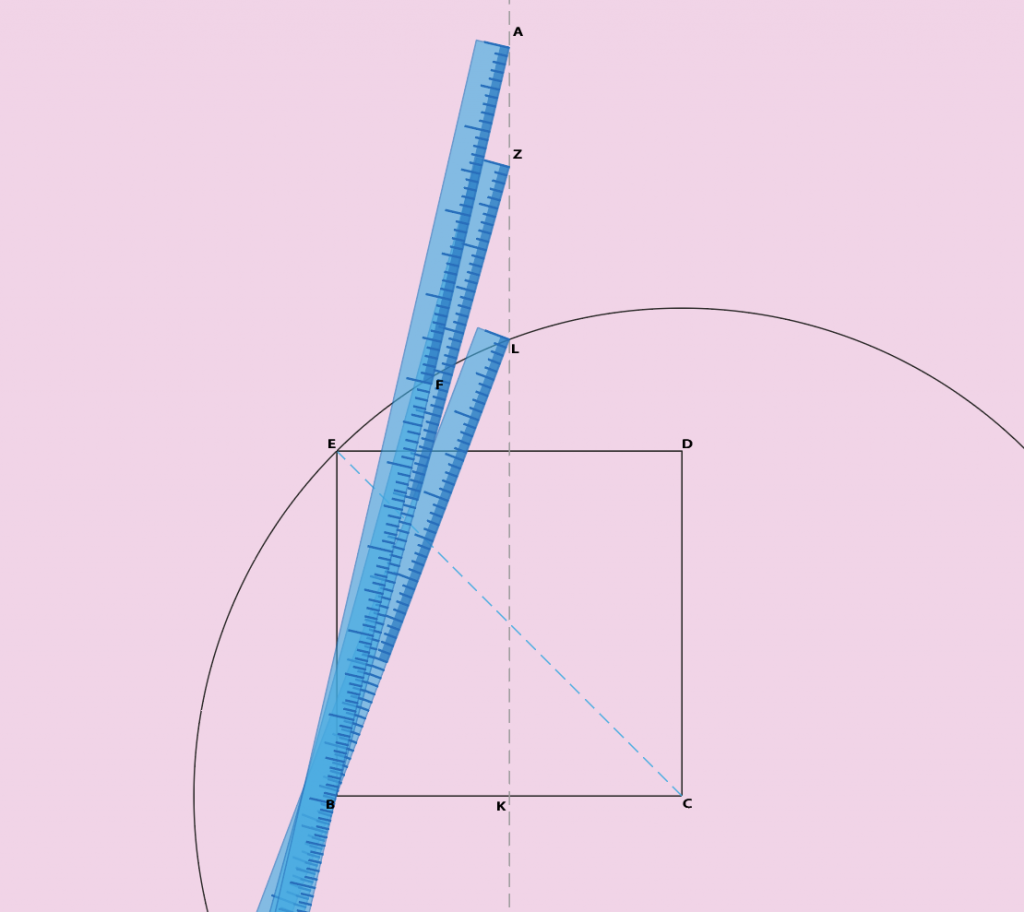
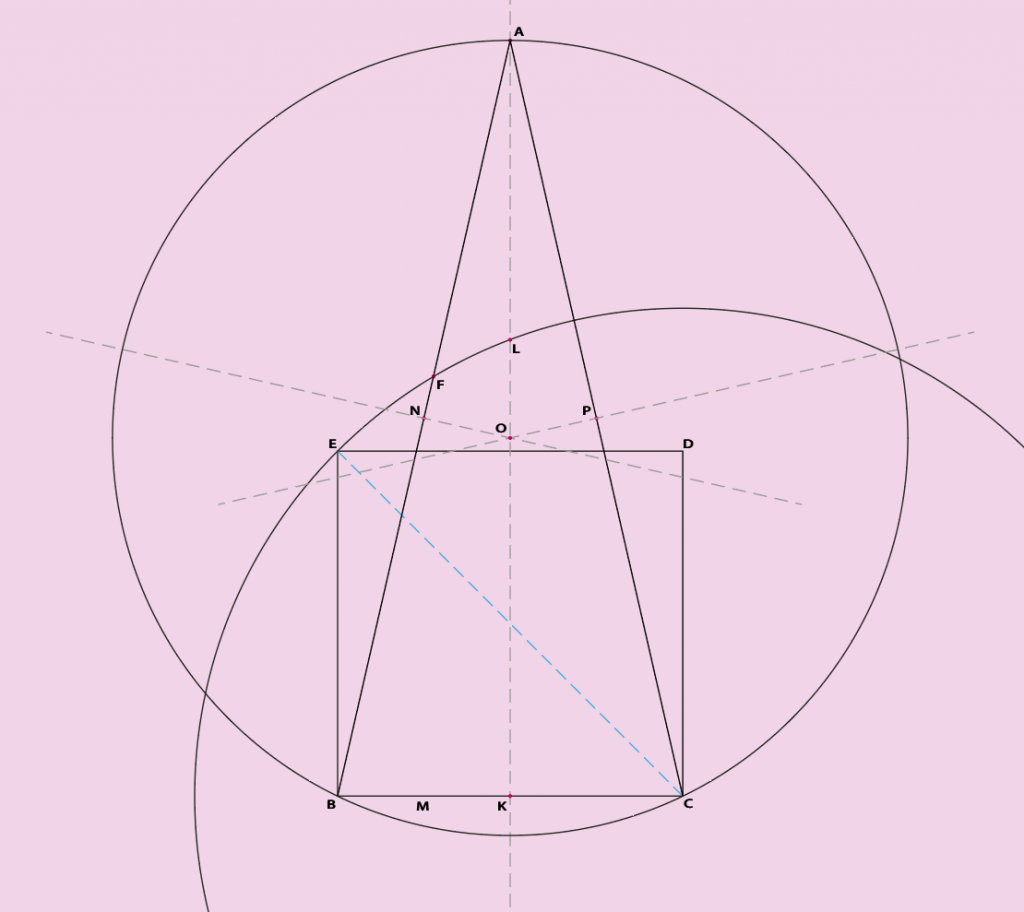
Ici on a un seul point fixe qui est B, on place donc notre règle quelque part en B et on met le début de notre règle quelque part sur la médiatrice KL. S’il faut choisir un point, on choisira L qui est à la fois sur notre cercle c1 et sur l’axe KL sur lequel on doit positionner A. On peut donc poser le début de notre règle sur ce point.

Donc au final et plus simplement que dit auparavant on positionne notre règle en L et on tourne autour de ce point jusqu’au point B. On remarquera que la distance LB est identique à LC car L est situé sur la médiatrice de BC.

Maintenant on va déplacer notre règle verticalement sur l’axe KL en direction de A (inconnu) en prenant soin que le point B soit toujours en contact avec la règle (voir graphique). On appellera Z ce point temporaire sur l’axe KL. On continue ce principe jusqu’à ce que l’on obtienne une distance AF — F étant notre point sur le cercle c1 — égale à BC. On aura mis un repère sur notre règle pour nous aider.

Astuce : vu que la distance AF = BC alors on peut faire un premier déplacement de BC / 2, faire son calcul et ajuster en conséquence la position. En partant d’un décalage du haut de ma règle de la moitié de BC, il me faut huit étapes pour arriver à avoir la bonne valeur de Z. On peut  maintenant appeller ce dernier point A.

Voilà. C’est fait; le point A est défini. Maintenant comment calculer le point F avec ce qu’on connait : voilà un truc que je ne sais pas encore faire !! Vais-je devoir réfléchir !!

On connait
• la position du point B
• la position du point A
• la position du point C
• la position du point K
• la position du point L

On sait que
• A est sur la médiatrice de BC donc la distance AB égale la distance AC
• l’angle BAK est le même que l’angle CAK.
• comme F est sur l’axe AB alors l’angle FAK est le même que BAK

On connait aussi
• la distance de C à F
• la distance BC
• l’angle FBC

Et comme on sait que AF = BC alors FC = AC – AF.

Après analyse, je suis maintenant en terrain connu. Comme j’ai les trois longueurs (BC, CF et FB) de mon triangle et un angle (FBC), l’angle BFM (M étant la projection de F sur BC suivant l’axe KL) est le même que l’angle BAK, je peux donc calculer le sinus et le cosinus de cet angle et pour trouver la position de F je n’ai plus qu’à trouver les distances BM et FM et les déduire ou les ajouter aux valeurs de B.

Voilà c’est fait on a notre point F situé sur le cercle c1 :
CF = CE = CL
A, B, et F sont alignés.

Je fais un aparté pour dire qu’il existe une méthode plus noble de construction des heptagones en utilisant les coniques mais il me semblait plus intéressant de montrer la méthode de construction par neusis pour son aspect plus empirique et plus adapté aux personnes avec moins de bagage mathématique. Cette méthode manuelle ancienne a été considérée comme l’une des pires méthodes par les mathématiciens au XVIII-XIXe siècles pour passer de l’art “abstrait et noble” des mathématiques vers une méthode ‘mécanique et terre-à-terre” mais bien utile sans aucun doute pour beaucoup d’artisans.

De plus, maintenant, avec l’informatique, il est possible de faire ce travail de règle déplacée de façon algorithmique en simulant le déplacement par augmentation ou réduction de la valeur de KA supérieure à KL pour obtenir notre distance BA, notre point F aligné sur BA et de vérifier la condition donnée AF = BC.

Bon revenons à nos moutons, leurs déplacements et les fleurs broutées sur ce chemin.

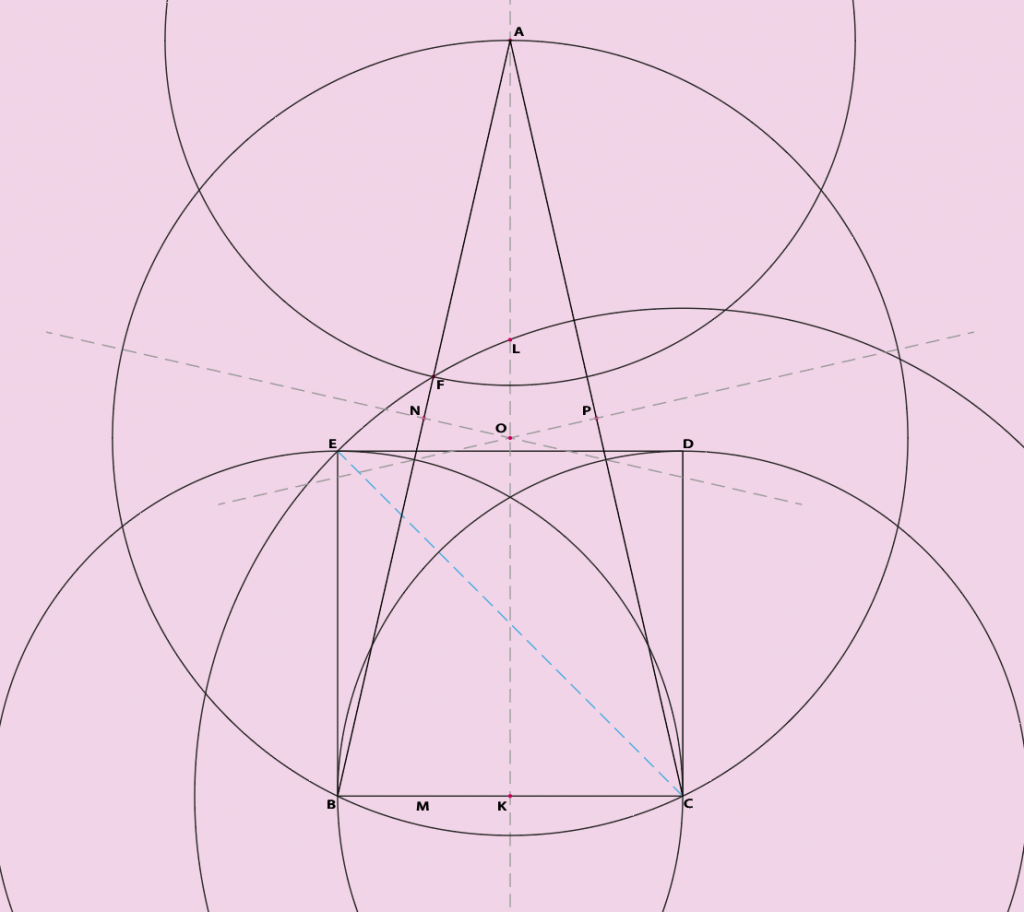
On avance en passant à l’étape suivante. On utilise pour cela la méthode du centre des médiatrices des segments des côtés du triangle.

Maintenant qu’on a la position de A, on doit calculer le rayon du cercle circonscrit ABC de centre O. O étant le point d’intersection des médiatrices de AB, BC et CA. Il nous suffit de deux médiatrices pour trouver ce point; la troisième ne servant qu’à vérifier notre calcul.

Comme on a déjà la médiatrice au coté BC il nous suffit d’en prendre une deuxième; la troisième nous servira seulement à vérifier notre calcul.

On connait déjà l’abscisse de O puisque O appartient à la droite KLA médiatrice de BC. On a donc la valeur x de O.

On calcule donc les coordonnées du point N centre de AB, puis on trace la perpendiculaire à AB passant par N. Cette droite croise normalement la médiatrice BC au point O qu’on va calculer.

On connait
• l’angle BAK
• la longueur de AB
• la position de N

et comme le triangle AOB est un triangle isocèle et que O est sur l’axe AK, on connait aussi
• l’angle BAO, identique à BAK
• l’angle ABO, identique à BAO.

Avec ses éléments, on peut calculer la dimension des segments AO et BO et la position y du point O. Il ne suffit plus qu’à dessiner le cercle c2 de centre O est de rayon OA passant par les points B et C.

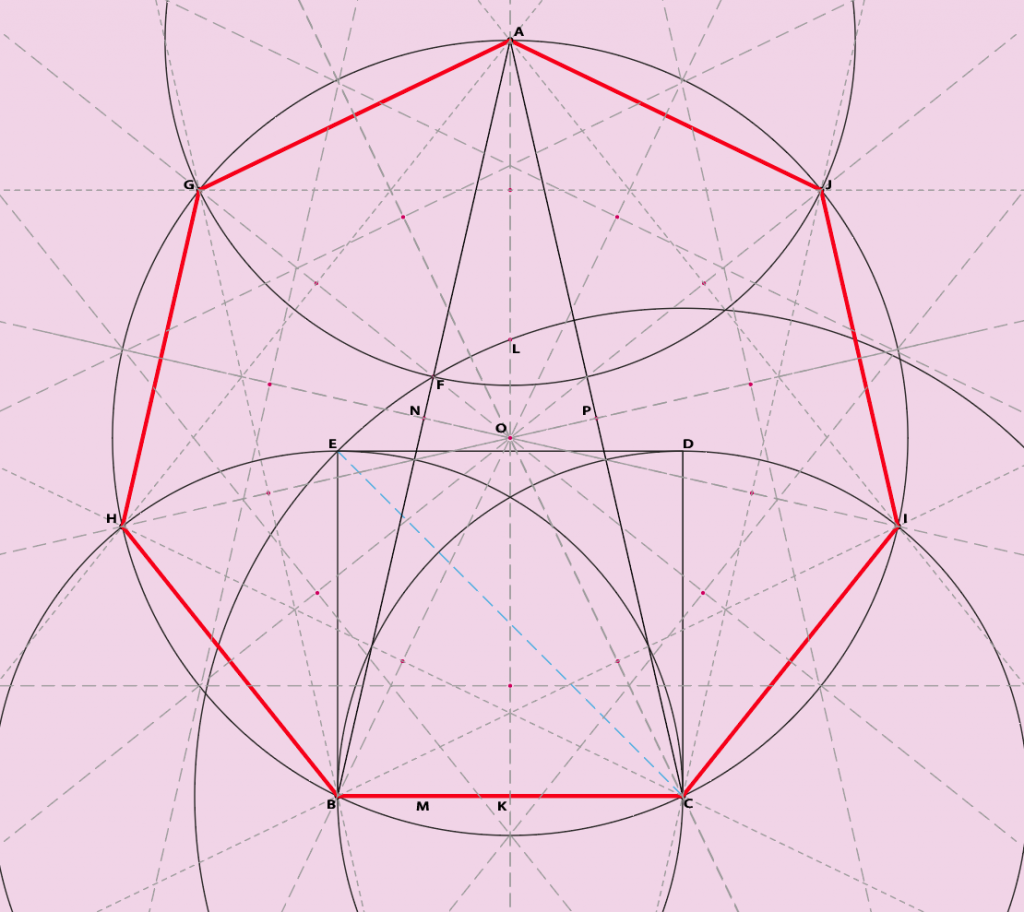
La dernière étape est la construction des autres points supports des autres cotés de l’heptagone.

Au compas, il suffit de tracer les cercles de rayon BC aux points présents du triangle ABC pour obtenir les quatre points supplémentaires au croisements de ces cercles avec c2.

Mathématiquement et informatiquement, on calculera les points manquants de la même manière qu’on a calculé les points du pentagone précédemment dans l’article Un peu de géométrie – partie 4.

Voilà on a terminé de dessiner notre heptagone régulier et ce n’est pas si mal en définitive. Pour des challenges plus imposants (et plus long en préparation, calculs, dessin et tout ce qu’on n’avait pas prévu, vous pouvez le faire pour les polygones plus importants.

Si le cœur vous en dit, internet vous donnera, j’en suis sûr, de plus ample informations là-dessus.

Pour en finir ponctuellement avec notre heptagone, On peut dire qu’il est peu utilisé en pavage de plan mais on peut trouver des motifs aussi bien dans la décoration et l’architecture islamiques et arabo-andalouses que dans l’architecture sacrée européenne (voir en références ci-dessous).

Les angles représentatifs de l’heptagone sont 51,42857°, 102,85714°, 25,71428°, 12,85714° et ses multiples.

La base de ces angles étant l’angle de 6,42857° avec une particularité qui pourra permettre le placement d’une formes basée sur l’heptagone. Le produit de 6,42857 * 7 nous donne un angle juste de 45* et 6,42857 * 8 nous donne l’angle de 51,42857° ce qui peut nous amener à cogiter sur les projections d’une forme dans un espace heptagonal ou octogonal.

Mais c’est une autre histoire.

Cette série est désormais finie, je vais revenir à un travail plus graphique dans mes prochains travaux.

À bientôt pour un nouvel article.

références :

La méthode par neusis : https://fr.wikipedia.org/wiki/Neusis

L’heptagone sur Wikipedia : https://fr.m.wikipedia.org/wiki/Heptagone

Quelques exemples de l’utilisation de formes basées sur le polygone à 7 angles.

Une architecture d’exception pour l’Église réformée de Ganges (Hérault) : https://journals.openedition.org/pds/2125

Le Pavillon des Sept Etoiles à Enghien (Belgique) : https://fr.wikipedia.org/wiki/Parc_d%27Enghien

Une rosace sur un mur de l’abbaye de Beaulieu-en-Rouergue : https://fr.m.wikipedia.org/wiki/Abbaye_de_Beaulieu-en-Rouergue

Église de l’Assomption de Rieux-Minervois : https://fr.wikipedia.org/wiki/%C3%89glise_de_l%27Assomption_de_Rieux-Minervois

La fontaine à ablutions heptagonale (et non pas hexagonale comme indiqué de l’ancienne mosquée de l’Ile de Kos (Grèce) : https://viagallica.com/grece/ville_kos_-_ville_ottomane.htm

L’heptagramme ou sceau des 7 archanges : https://www.france-mineraux.fr/geometrie-sacree/sceau-des-7-archanges/