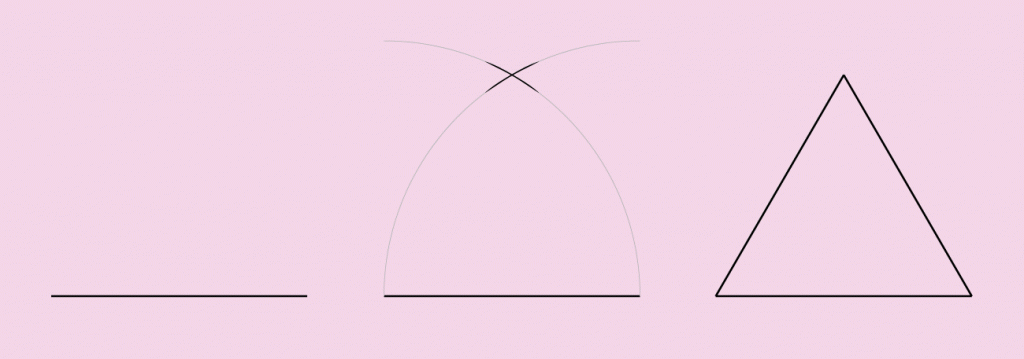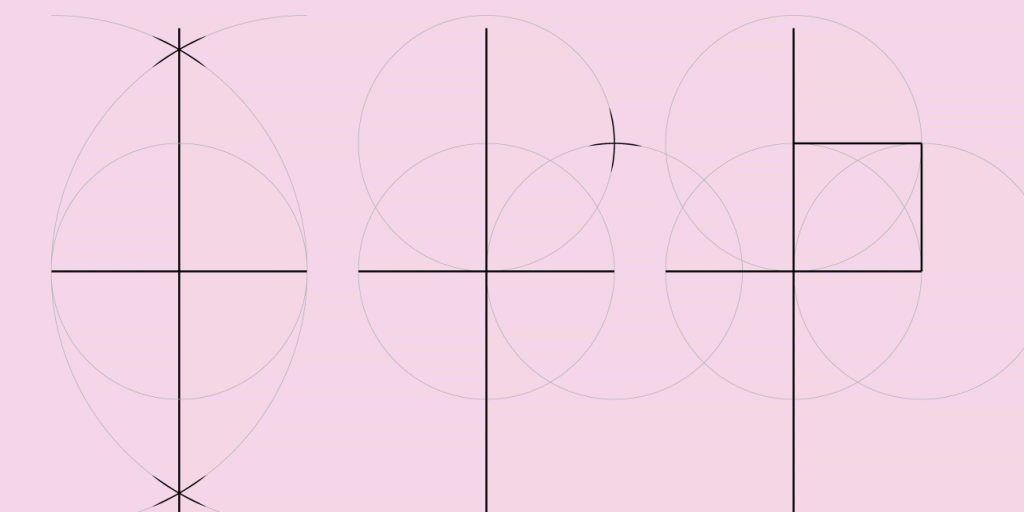Après une introduction déjà bien chargée en informations on passe maintenant dans le vif du sujet.

Que faut-il pour dessiner une forme ?

Ceci est la suite de l’article Un peu de géométrie – partie 1

J’ai réalisé de façon simple dans Illustrator un triangle que j’ai dupliqué, déplacé, retourné et ensuite grâce à quelques automatismes, j’ai ajouté à celui-ci une multitude de segments passant par un point caractéristique pour arriver à un autre point caractéristique et le dépassant jusqu’à l’infini et au-delà. Mais comment il y a quatre millénaires dessinait-on avec précision ces formes ?

Les origines de la géométrie sont multiples : Égypte, Inde, Mésopotamie. La plus ancienne pyramide d’Égypte a près de 4700 ans mais il est maintenant sûr qu’au Mexique à la même période, on en construisait aussi.

Pour arriver à ériger des monuments de 100 m et plus de hauteur, il fallait certainement des connaissances profondes de certains principes dont les principes géométriques. La création d’outils spécifiques pour mesurer et dessiner avant de construire a dû justement permettre l’essor des sociétés primitives. De la construction d’un enclos à celle d’une pyramide, il n’y avait qu’un pas franchi certainement sur 10 000 ans ou plus.

En Turquie, il y a 12 000 ans on fabriquait déjà des statues monumentales qu’on fichait en terre à la verticale auprès de bancs en pierre, eux parfaitement à l’horizontale (site de Göbekli Tepe). Ces statues pouvaient servir à soutenir un toit lui-même construit avec des notions de géométrie importantes.

Si les hommes ont utilisé leurs mains pour les premières mesures ou les premiers calculs, ils ont dû les utiliser aussi pour dessiner, il ne leur a suffit que d’utiliser leur environnement pour faire évoluer ces techniques et pouvoir augmenter les nombres calculées, les dimensions mesurées, les surfaces circonscrites. Cela a donné naissance aux deux outils indispensables de tout bâtisseur et mesureur : la règle et le compas.

Si on attribue l’invention du compas aux égyptiens vers 1 600 avant notre ère, je ne doute pas que cet objet servait déjà sous une forme moins stéréotypé des millénaires auparavant par l’utilisation de quelques bouts de bois noués entre eux par des bouts de tiges de certaines plantes ou par les nerfs de certains animaux. Pour la règle pareil, de la main on est passé à la tige solide puis certainement à la corde à nœud pour mesurer tout ce qui pouvait en avoir besoin. Cela en grande partie pour la construction de bâtiments qu’ils soient collectifs ou individuel plus tard avec l’augmentation de la notion de propriété. Il reste d’ailleurs dans le système anglo-saxon les références à ces usages :  inch (pouce), foot (pied), palm (paume), hand (main), ell (coudée) se rapportant au corps humain; yard (verge), rod (tige), perch (perche) à nos bouts de bois. Je ne les nomme pas toutes et ces unités de mesures ont aussi servi en construction jusqu’au XIXème siècle en France.

On peut ajouter à ces deux instruments deux autres outils d’utilité universelle qui sont le fil à plomb qui permettait d’ériger un poteau « angulus rectus » soit à angle droit du sol et l’équerre. je met cet instrument en dernier car pour créer une équerre, il aura fallu dans les temps anciens faire preuve d’un peu de jugeote en utilisant soit un compas soit un fil à plomb. L’ensemble des deux méthodes venant prouver quelque chose, du moins intuitivement au moment de cette découverte.

Vous aurez remarqué que ces outils en plus d’être universels sont l’apanage de quelques corps de métier ou quelque société secrète les utilisant. Se pourrait-il que la considération de ces outils soient symboliquement représentative pour leurs membres de leur usage pour la compréhension de l’univers ou de ce qui a amené l’homo erectus à devenir l’homo sapiens. Ce serait une pensée contemporaine car à l’époque où sont nées ces sociétés ces notions d’évolution de l’homme dans le sens darwinien n’étaient pas d’actualités.

D’autres outils ont certainement été utilisés auparavant pour des usages plus primaires comme chasser, manger, se vêtir, se protéger mais il est sûr que le compas et l’équerre sont représentatifs de l’intelligence telle qu’elle est perçue dans notre époque moderne.

Après cette introduction chargée en informations (voir liens en références ci-dessous), je reprends ma question : « Que faut-il pour dessiner une forme ? ».

La première forme est le triangle équilatéral et le dessiner n’est au final pas très compliqué. Qu’on prenne trois allumettes, trois crayons identiques, trois bouts de bois de la même taille, on obtiendra toujours un triangle équilatéral en reliant leurs bouts deux à deux. avec une règle et un compas, il suffit au départ de dessiner un segment de droite, puis de l’utiliser de façon à trouver le juste écartement pour notre compas. Prendre comme centre un des bouts de ce segment, de dessiner un arc de cercle d’un coté de notre segment, puis de faire la même chose en utilisant l’autre bout et en redessinant notre arc de cercle du même coté que le premier. il suffira ensuite de dessiner les deux segments de droite manquants en utilisant comme bouts de ceux-ci les bouts de notre premier segment et le point d’intersection de nos arcs de cercle (voir la figure ci-dessus).

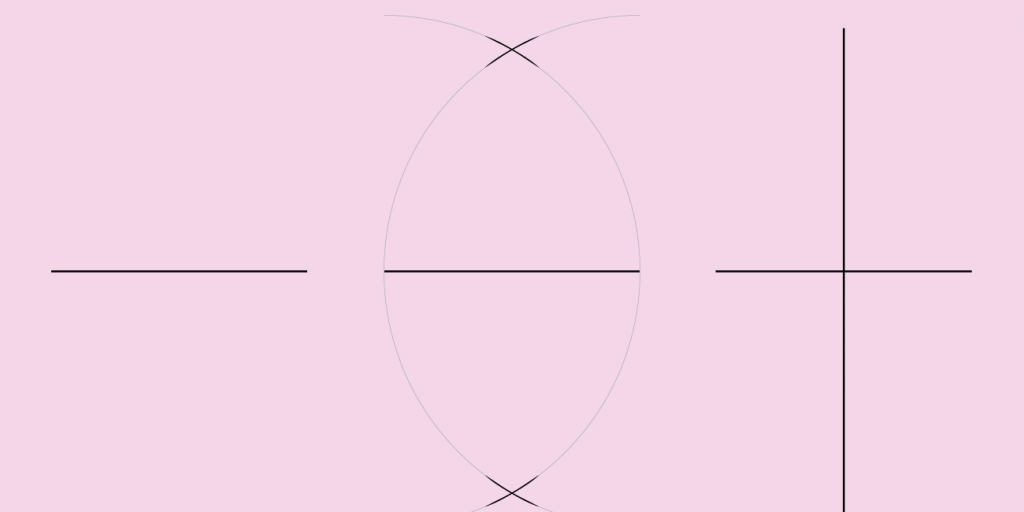
Ensuite le pas est vite sauté en appliquant une deuxième fois cette méthode et de dessiner la ligne entre les deux intersections pour obtenir notre fameuse perpendiculaire et notre angle droit. Il suffit donc à partir de là de créer un outil de deux bout de bois de le consolider avec un troisième au niveau de l’angle et notre équerre primitive a surement son origine beaucoup plus tôt qu’on ne le pense. Il suffit de voir sur les murs des temples égyptiens ces équerres et compas pour le subodorer.

Si à cette époque éloignée, j’avais eu devant moi cette première évidence, aurais-je cherché à aller plus loin ? À trouver autre chose ? Certainement que de là est venue la deuxième création d’une forme géométrique : le carré.

J’ai tracé ma ligne, grossièrement sa perpendiculaire avec mon compas, je me retrouve avec une croix (qui peut aussi être considérée comme une forme même si ce n’est pas au sens mathématique) et il y a un endroit qui m’attire sur ce graphique le point de croisement de mes deux lignes. Je reprend mon compas, j’ajuste le rayon au segment de trait le plus court, je dessine mon cercle, je déplace mon point central sur un des nouveaux croisements entre mon cercle et mes lignes, je fais cela plusieurs fois et j’ai une figure de plus en plus complexe qui se dessine. Je retrouve un point de croisement de deux cercles que je marque et je trace deux lignes perpendiculaires de mes deux lignes en croix à mon nouveau point de croisement et j’ai maintenant une nouvelle forme visible : mon carré.

Il suffirait maintenant de reprendre encore une fois notre compas, de dessiner un cercle dont le rayon serait la longueur de notre point central au nouveau point dessiné et alors là, on pourrait facilement passer du carré au rectangle. Un rectangle de taille 1 x √2 mais là on aborde d’autres notions, d’autres temps, d’autres mathématiques.

Quelques centaines d’années avant J.C, les tribus celtes présentes en Europe ont utilisé le compas pour réaliser des phalères (sortes d’ornements guerriers généralement ronds) métalliques dessinées de motifs circulaires entremêlés. L’usage comme décoration militaire et pour l’ornementation des chevaux était commune. L’enchevêtrement de ces cercles avait-il une raison ou était-il purement décoratif ? On a ici un usage particulier du cercle qui vaut qu’on s’y attarde.

Quelques milliers d’années avant, les hommes utilisaient déjà des racloirs en bronze. Ces racloirs étaient entre autre de formes triangulaires, ce qui peut interpeler mais peut-être était-ce la forme la plus simple et la plus ergonomique trouvée pour cet objet et cet usage.

La plupart des connaissances sont généralement issues de la recherche d’un moyen d’éxécuter une tâche ou alors du domaine du hasard l’usage venant ensuite. La géométrie n’y fait pas abstraction.

Suite de l’article ici : Un peu de géométrie – partie 3

références

Qui a inventé le compas ? https://qui.galerie-creation.com/_s/qui-a-invente-le-compas/1292171/