Maurits Cornelis Escher est un artiste néerlandais décédé en 1972. Sa spécialité était le dessin monochrome, la gravure sur bois, la lithographie et la xylographie, Le principe d’une partie des travaux de MC Escher est la symétrie, l’illusion et le pavage du plan. Il rejoint en cela Victor Vasarely même si leurs techniques étaient complètement différentes car le travail de la couleur est peu présent sinon discrète dans l’œuvre de MC Escher et ce dernier bien qu’intégrant les mathématiques dans son travail est resté un figuratif alors que Vasarely a tout misé sur la représentation géométrique.

Après un passage en Italie à dessiner les paysages de campagne — pays duquel il est parti à cause de la montée du fascisme — c’est en visitant le sud de l’Espagne que MC Escher a trouvé sa vocation. Dessinateur déjà aguerri de par sa formation dans les arts décoratifs, il est impressionné de voir sur les murs de l’Alhambra l’imbrication de ces milliers de petites pièces. Le résultat de motifs à la fois répétitifs et différents à chaque fois l’interpelle.

On dit qu’il est resté trois jours à dessiner ces motifs, à vouloir les reproduire à la main comme tout dessinateur confirmé qu’il était et je le crois fortement y passant moi-même des journées complètes alors que je dessine sur ordinateur, n’ayant jamais eu la main assurée et précise.

Aujourd’hui, je vais expliquer un peu le principe des déformations d’une pièce pour arriver à une forme reproductible et imbriquable à l’infini. Je partirai de la forme la plus simple (le carré) pour la déformer peu à peu. Je ne sais pas encore où j’arriverai faisant confiance à mon inspiration de la journée. Je laisserai sur le papier (l’écran !) la trace de ce travail et j’espère en tirer quelque amusement et approfondissement pour moi et stimuler votre esprit de ces découvertes.

Nous allons commencer par montrer visuellement comment on peut, à partir d’une pièce simple, la déformer en conservant ces principes. Le principe du pavage du plan est qu’à partir d’une figure simple on arrive à recouvrir tout l’espace — le plan ici — avec cette pièce et sans intervalle. Bien sûr, on s’arrêtera comme souvent en mathématiques après quelques figures, laissant le lecteur imaginer l’infini. En figure 1, je pars d’un carré simple et j’altère ce carré en y prélevant un triangle que je replace ailleurs et je répète cela plusieurs fois. Il faut bien penser lorsqu’on fait ces manipulations à la pièce d’à coté. Ce que le coté gauche perd ou gagne le coté droit doit faire de même mais à l’inverse.

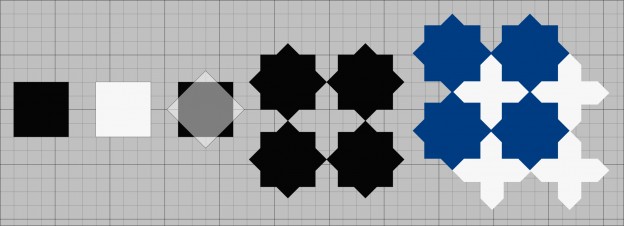
Une autre possibilité est de transférer les éléments que l’on enlève à la forme d’à coté. On part de deux carrés et on arrive à tout à fait autre chose. À l’inverse, on peut prendre 2 pièces quelconques pavant le plan et en les manipulant il y a fort à parier qu’on puisse retomber sur la pièce originale qu’elle soit un carré, un rectangle, un triangle ou toute autre forme avec les même propriétés. Dans l’art de la zellige la pièce de base est le « khatem », le sceau, il s’agit d’une pièce en forme d’étoile à huit branches. Pour réaliser cette pièce, c’est simple; la technique est la même que pour dessiner le sceau de Salomon; vous prenez un carré, vous le dupliquez en le laissant à la même place dans une superposition parfaite puis vous faites tourner ce carré en son centre de 45°, un huitième de tour… Et vous avez votre étoile. Puis vous dupliquez cette étoile et la déplacez latéralement en les mettant bord à bord par l’un de leurs rayons ou sommets en géométrie. En dernier, vous prenez ces deux étoiles, les dupliquez et glissez les deux nouvelles étoiles verticalement de la même façon en les mettant sommet contre sommet. Maintenant que ces quatre formes sont en place, vous devriez voir un espace central vide en forme de croix, cette croix est la représentation de ce que je venais de dire avant. Assemblés, la croix et le soleil ont la même surface que les deux carrés d’origine qu’on a utilisés au départ pour réaliser le soleil. Les deux formes s’imbriquent parfaitement pour former le motif bleu et blanc de mon article précédent « Zelliges et encore zelliges« .

Ces deux pièces pourraient se réaliser autrement. En figure 3, je montre les découpes et déplacements à faire pour arriver à former les deux pièces. Cela démontrera toujours mieux cette histoire de pavage de plan qui n’est somme toute qu’une histoire de triangles déplacés.

Maintenant que j’ai montré comment modifier une forme ou comment assembler une ou plusieurs formes pour remplir le plan. J’en reviens à MC Escher. Lorsqu’il a vu le pavage de zelliges sur les murs du château de l’Alhambra de Grenade, ça n’a pas dû faire ding-dong de suite. L’idée n’a certainement pas germé instantanément dans son esprit de réaliser des dessins répétitifs en utilisant la technique du pavage de plan. Plus tard, il s’est lié d’amitié avec Roger Penrose, l’un des mathématiciens du XXème siècle ayant le plus travaillé sur le pavage du plan. Ensemble ils ont dû avoir pas mal de conversations sur ce sujet et passer certaines soirées l’un à étonner l’autre par un dessin délicat et l’autre à faire de même par l’écriture d’une formule résolvant un problème soumis par le premier.

Mc Escher n’a pas seulement utilisé le savoir de Penrose en mathématique, il a utilisé une forme très caractéristique trouvée par le mathématicien August Ferdinand Möbius au XiXème siècle, une surface non orientable à deux dimensions avec seulement une face quand elle est plongée dans un espace euclidien à trois dimensions (comprenne qui pourra), il s’agit ben sûr du ruban de Möbius (ou Mœbius, Moebius). Il a aussi dessiné de nombreuses fois le cube de Necker du mathématicien et cristallographe de même nom. Et je me prends à penser qu’il a peut-être pu aider Penrose dans ces travaux sur le triangle de Penrose. Sur ces trois formes, une seule peut-être fabriquée, le ruban, les deux autres sont des illusions d’optiques seulement compréhensibles ou du moins démontrables par les mathématiques. Escher a parsemé son œuvre d’objets mathématiques comme par exemple le dodécaèdre étoilé et vous remarquerez dans ce dernier objet l’usage des triangles dont je vous parle tant.

Malgré l’usage des mathématiques l’œuvre de Maurits Cornelis Escher est resté à taille humaine, même si on a de la difficulté à saisir le contexte mathématique, ces dessins sont tous de l’ordre de la représentation imagée et d’une beauté par la finesse des traits et la palette de couleurs utilisée. C’est à la fois un antagoniste de Victor Vasarely et malgré cela, ils avaient un but commun : faire aimer par l’art les mathématiques et la géométrie. Je pense qu’ils y sont arrivés (du moins pour moi).

PS : du fait des droits d’auteurs,  je ne mets pas de représentation d’œuvres de MC Escher mais je vous amène à faire une recherche Google et à en savoir plus sur celui-ci. On pourrait presque dire qu’il met aussi une forme d’humour dans ces dessins. Je suis sûr que vous aimerez.